In a sense, mathematics is a study of quantity, pattern and structure; whereas the basis of science is empiricism. Throughout history, as humans observed something in the natural world, we would try to create our own model of how it worked or occurred. Basically, we would try to convert that which we observed into its mathematical essence. When successful, we leveraged the new math to create and engineer new things. Throughout history, human beings have studied science, and the mathematics derived from it, to think critically and understand the world around us. Along the way, we have realized that nature’s math can also be poetic and beautiful.
Fibonacci Sequence
In nature, mathematics is ubiquitous. If one were to break down the arrangement of the petals on a daisy, Romanesque broccoli spirals, or the ordering system of a pinecone, one would arrive at common and related mathematical sequences. Around the turn of the thirteenth century, Italian mathematician Leonardo Fibonacci observed that many patterns in nature are seemingly derived from a basic mathematical order by which two consecutive numbers in a sequence are added together to yield the next number in the sequence:
1+1 = 2
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
8+13 = 21
and so on…
Coined the Fibonacci sequence (or Fibonacci number if referencing one integer), this numerical sequence appears so much in nature that it almost seems to be a governing ordering principle:
Petals of Flowers
It is very common for flowers to exhibit a number of petals consistent with a Fibonacci number. For example, buttercups have five petals, lilies and irises each have three petals, corn marigolds have 13 petals, some asters have 21 whereas daisies can be found with 34, 55 or even 89 petals.
Succulents
When a plant has spirals, the rotation will usually be a fraction made with two successive Fibonacci numbers such as 1/2 or 3/5 or 5/8. This rotation allows layered petals to not obstruct sunlight and rain from each other.
Tree Branches
The growth pattern of many species of trees have been observed to adhere to a Fibonacci-like sequence.
Golden Ratio (or Proportion)
If one were to add up the square roots of the Fibonacci sequence, an interesting pattern is revealed.
12 + 12 + 22 + 32 + 52 + 82 = 104 = 8 x 13
or
1 + 1 + 4 + 9 + 25 + 64 = 104 = 8 x 13
The 8:13 ratio – which can also be expressed as 1:1.618 – is often referred to as the golden ratio (or golden proportion, golden mean, even golden section). Two quantities are in the golden proportion if their ratio is the same as the ratio of their sum to the larger of the two quantities.
The unique properties of the golden ratio provide another example. A rectangle in which the ratio of the sides a/b equate to the golden proportion, can result in a nesting process that can be repeated infinitely – and also takes on the form of a spiral. It is often referred to as the logarithmic spiral, and it abounds in nature.
Nautilus Shell
This is the most classic example of the golden ratio articulated in nature via the logarithmic spiral.
Seed Heads
Typically, seeds are produced from a center and then migrate outward in related logarithmic spirals. Sunflowers are great examples of this.
Galaxies
Even the entire universe. The logarithmic spiral is a consistent ordering system throughout the cosmos.
Experiments in Architecture
Architects have utilized the golden ratio for centuries (e.g. the Parthenon or Le Corbusier’s United Nations Secretariat Building), especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio. Believing this proportion to be aesthetically pleasing, the golden ratio has often been referred to as the “harmonic proportion,” as illustrated in Figure 1.
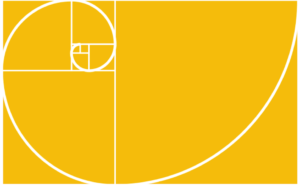
Figure 1: In mathematics, two quantities are in the golden proportion if their ratio is the same as the ratio of their sum to the larger of the two quantities. This figure illustrates the geometric relationship, often referred to as the golden rectangle or “harmonic proportion.” Illustration by Daniel Overbey.
Numeric Reduction Technique
The Fibonacci sequence can also be applied to the numeric reduction technique to reveal yet another mathematical relationship.
Numeric reduction is a technique used in the analysis of numbers in which all the digits of a number are added together until only one digit remains. For example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying the numeric reduction technique to the Fibonacci sequence produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
Recurrence of Nine
If one were to take the first twelve digits and add them to the second twelve digits and apply numeric reduction to the results, you find that they all have a value of nine. Add all 24 numbers in the sequence and you’ll arrive at 117, which also breaks down to 1+1+7 = 9.
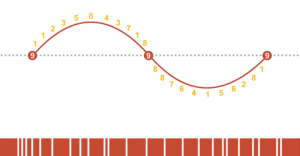
Sine Wave
Again, let us pair the first dozen numbers to the second dozen in the sequence. Notice each number in the series is directly opposite its inverted pair. This allows us to look at the cycle as a sine wave. When the wave dips downward, the numbers repeat in an inverted sequence – that is, subtracted from 9.
1, 1, 2, 3, 5… is inverted as 8, 8, 7, 6, 4…
This sine wave is an ordering system found commonly in nature:
Light and Sound Waves
A sinusoidal relationship is clearly discerned from the principles of electromagnetic frequencies and the undulations of molecular compression caused by sound energy.
Nucleic Acid Double Helix
The structure of deoxyribonucleic acid (DNA) is often referred to as a double helix, which resembles a twisted staircase. This is an example of a complex arrangement of multiple sinusoidal arrangements.
Sun Path
The diurnal movement of the Sun across the Earth’s sky adheres to a sinusoidal order.
Figure 2 articulates the sinusoidal representation of the Fibonacci sequence applied to the numeric reduction technique; whereas Figure 3 illustrates segments proportioned by the 24-number series.
Figures 4 – 6, provide an example of how such a pattern derived from the Fibonacci sequence was leveraged as a harmonic and unifying design solution for a major renovation and expansion project underway at Butler University.
Numbers are All Around Us
The Greek philosopher Pythagoras of Samos contended, “Numbers rule the universe.” Indeed, it seems that mathematics is omnipresent in our day-to-day lives. We are constantly inundated with quantities and measurements. The first and last thing many of us see every day is a number on an alarm clock or phone. Yet, it also seems that to some degree nature itself is grounded in mathematics. Throughout recorded history the greatest human minds saw mathematics as the key to understanding the universe. Italian Astronomer Galileo Galilei once asserted that “Mathematics is the language in which God has written the universe.” Moreover, as humans have come to better understand the order of nature, we have awakened to the intrinsic harmony of the world around us. As British philosopher Bertrand Russell once said, “Mathematics, rightly viewed, possesses not only truth, but supreme beauty.”
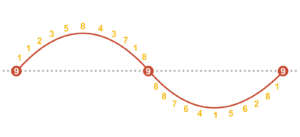
Figure 2: The sinusoidal representation of the Fibonacci sequence applied to the numeric reduction technique. Illustration by Daniel Overbey.
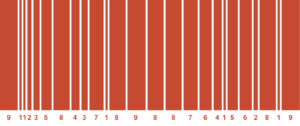
Figure 3: Segments proportioned in accordance with the repeating 24-number series derived by applying the numeric reduction technique to the Fibonacci sequence. Illustration by Daniel Overbey.

Figure 4: Inspired by the science, rhythm, and proportion of nature, the design team for the Butler University Center for the Science stitched together the existing facilities and new addition of the 250,000-square-foot project with a glazing system that expresses the harmonic rhythm of the Fibonacci sequence when applied to the numeric reduction technique. South view illustration by BSA LifeStructures and Browning Day Mullins Dierdorf.

Figure 5: A view of the new addition planned for the Butler University Center for the Sciences. The pattern derived from the Fibonacci sequence is expressed through both the glazing system as well as the insulated precast concrete panels. North view illustration by BSA LifeStructures and Browning Day Mullins Dierdorf.
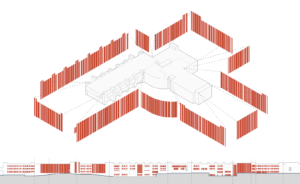
Figure 6: The pattern derived from the Fibonacci sequence is an infinitely repeating 24-number sequence. The pattern was scaled and applied across the entire perimeter of the existing facilities and new addition. The rhythm of the pattern expressed through a complete re-glazing of the Butler University Center for the Sciences, will serve as a harmonizing design element that pays homage to the ordering principles of nature revealed through the scientific disciplines. Illustration by Browning Day Mullins Dierdorf.
Daniel Overbey
AIA, LEED Fellow, WELL AP






